Fixing an Overheating USB Hub

So I've had a Belkin F5U237v1 USB 2.0 7-port powered hub for quite some time.  It's a pretty nice little hub to have; I especially like the top USB ports and the fact that I can charge USB devices from it without needing the computer turned on.

However, occasionally I've noticed it stops working entirely when I either (i) plug lots of stuff into it for a long time, or, (ii) when I'm doing something fairly intensive across it for a prolonged period of time (large file transfers to portable USB disks etc).

This hub has long since passed it's warranty and I didn't particularly feel like shelling out for a new one when this is fine 95% of the time.  However, I did notice that gets really hot to the touch just before it stops working.

Anyway, let's open it up:

The screws are under the four little feet on the base.  After they are out the entire thing just snaps apart without any problem.  It's made up of just one circuit board, which isn't secured to the case, so it's pretty hard to break anything.  The visor at the front, covering the LEDs, will fall out so make sure you don't lose it.

The majority of the heat seems to be coming from the power transistor on the left (labelled UTC 2N2955) with a smaller amount coming from the diagonally mounted chip on the right.  As the transistor heats up the amount of power it will be able to disipate will decrease - my guess is that the hub gets hot enough that the transistor can't cope with the load any more and it all stops working.

The internals don't look great for cooling.  It's an enclosed area with no airflow and a plastic shell acting as an insulator.  Letting it breathe a little bit should help.

Excuse the terrible drill work - I started trying to do this just using a masonry drill bit which didn't go terribly well - switched to a tile bit to do the slightly nicer holes.  Function over form anyway! The aim here is just to punch some holes in the plastic shell to let hot air out and, hopefully, cooler air in near the two hottest components.  This should keep the whole unit a little cooler.

Putting it all back together, remembering to put the LED visor in, it doesn't look too bad; even with my poor drilling work.  It's actually even less noticable in practice as I artificially lit the scene for the camera - this sits behind my monitor in the shade where the holes are virtually invisible.

Importantly, the hub runs a lot cooler to the touch which has hopefully solved my problem (at the very least it's not done it yet despite some fairly extensive testing).  If you do something like this on your own hub I imagine it'll void any warranty you might have.

Cellular Senescence and Genome Wide Methylation Analysis

Recently we conducted a study into the pattern of methylation within senescent cells.

Senescence

Senescence is the permanent halt of proliferation associated with cellular stresses including DNA damage, damaged or short telomeres and oxidative stress.  Senescence dates back to the Hayflick limit and, while there are no definitive markers, cells typically become large and flat and can be identified by the presence of SA-β-GAL, SAHF and tumour suppression networks (i.e. p53 / p16).

Senescence is thought to be a tumour suppression mechanism, through blocking clonal proliferation of cancer cells, and a promoter of ageing via an inflammaging phenotype.  Cancer cells must somehow bypass senescence in order to continue proliferating.

Methylation 

We were interested in studying genome-wide DNA methylation patterns within senescence.  DNA methylation is the addition of a Methyl group to specific DNA bases.  In mammals this is restricted to the cytosine nucleotide (C) within DNA.  Methylation is largely localised at CpG's (a cytosine nucleotide followed by a guamine nucleotide) within the genome.

In order to study DNA methylation we use whole genome sequencing combined with bisulphite treatment.  Bisulphite treatment of DNA converts unmethylated cytosines into uracil - when we apply a process known as polymerase chain reaction (PCR) to the DNA before sequencing this is then further converted into thymine.  Methylated cytosines are unaffected.  Therefore, when sequencing a methylated cytosine will be read as a cytosine while an unmethylated cytosine will be read as a thymine.  As such when we sequence the DNA we can then deduce, via comparison with the human reference genome, which cytosine nucleotides were originally methylated and which were unmethylated.

Loss of Methylation at Late Replicating Regions

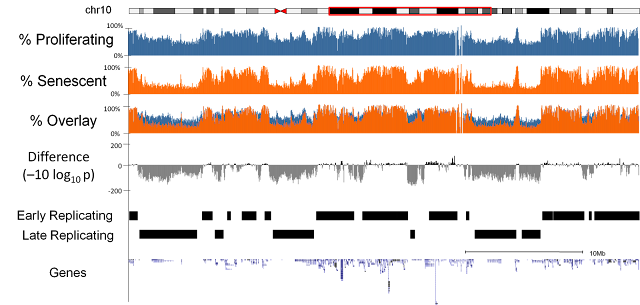
We sequenced three replicates of proliferating and replicative senescent cells (IMR90 cell culture). Our first observation was that there was a general loss of methylation (hypo-methylation) within the cells and that this loss was focused at regions of the genome which were only partially methylated (as opposed to completely unmethylated or fully methylated).  Further investigation highlighted a relationship with the regions losing methylation and late replicating regions of the genome.  i.e. regions of the genome where DNA is replicated later on during the cell cycle[1].

Focal Hypermethylation

We observed that methylation does not globally regulate gene expression changes but we did detect a subset of genes with very similar patterns in terms of methylation changes and which were coregulated at the expression level. In these genes we observed focal increase in methylation (hyper-methylation) at the regions adjacent to islands of high CpG content and that these genes were frequently associated with cell cycle functions.

Relationship to Cancer

Surprisingly, considering the role of senescence as a tumour suppression mechanism, we discovered that the methylation changes in senescence were very similar to the methylation changes that had previously been described in cancers[2,3,4].

Origins

We discovered that the origin of the loss of methylation appeared to be due to mislocalisation of the DNMT1 methyltransferase which is responsible for propagating the original methylation pattern of DNA at replication.  Specifically we noticed that foci of the DNMT1 protein are lost in old cycling cells and that these foci had previously been linked to late replicating regions[5].

Bypassing Senescence

Finally, we bypassed senescence via the introduction of SV40 T antigen into the cells in order to deactivate tumour suppression networks.  This allows the cells to continue proliferating, for a period of time, beyond the usual senescence time limit.  When we did this we made the same measurements of DNA methylation as before and found that the methylation changes that occur on the path to senescence are retained in the bypass cells.

Conclusion 

We therefore conclude that the failure of DNMT1 to methylate late replicating regions in near senescent cells may be the origin of the same methylation patterns found in cancer cells.  Furthermore, given the similarities, it may be possible that these changes may lead cells to be more susceptible to transformation into cancer cells.

The full paper is available online from Nature Cell Biology, is discussed by a CRUK press release and the raw data is available from GEO GSE48580.

References

[1] R. S. Hansen et al., Sequencing newly replicated DNA reveals widespread plasticity in human replication timing, PNAS, 2010.

[2] K. D. Hansen et al., Increased methylation variation in epigenetic domains across cancer types, Nature Genetics, 2011.

[3] B. P. Berman et al., Regions of focal DNA hypermethylation and long-range hypomethylation in colorectal cancer coincide with nuclear lamina–associated domains, Nature Genetics, 2012.

[4] G. C. Hon et al., Global DNA hypomethylation coupled to repressive chromatin domain formation and gene silencing in breast cancer. Genome Research, 2012.

[5] L. Schermelleh  et al., Dynamics of Dnmt1 interaction with the replication machinery and its role in postreplicative maintenance of DNA methylation. Nucleic Acids Res, 2007.

What is a replicate anyway?

In science we perform replication as the primary way of ensuring reproducibility. This is one of the key principles. Science only advances through consensus - initially within a single lab and later within the scientific community at large.

However,  there are lots of different ways the replicates can be performed in any given experiment and the choice depends on exactly what experimental conditions you are trying to control for.

In this post I will argue there is a hierarchy of replication which should be considered when planning any scientific experiment.  For the purposes of this post I will use experiments within the molecular biology domain to illustrate my points but I believe it is applicable into other fields.

Technical replicates

Technical replicates are aimed at solving the problem of inaccurate measuring devices.  No measuring device is perfect and they will produce slightly different answers each time you use them.

A typical example of technical replication might be to measure the RNA abundance of a particular gene three times on a single sample.  Subsequently this allows you to make a higher confidence estimate of the actual abundance of the sample - specifically it allows you to actually estimate the degree of error in the measurement. i.e. How accurate is your gene expression abundance measurement anyway?

Experimental replicates

Experimental replicates are used to detect the degree of variation that is introduced by a particular instance of an experiment.  If any given experiment is repeated on a different day it will have slightly different results from the original.  Experimental replicates are there to figure out exactly how big an effect this has on your experimental observations.  Experimental replicates may well be performed on the same tissue sample or cell line if the aim is to show the effect of a particular treatment is consistent for a sample.

Examples of things that might influence how well an experiment replicates on different days might include environmental effects such as ambient temperature, the experimenters mood (and subsequently how careful they were) or how many interruptions they had and when they were.

Biological replicates

Next up is biological replication which aims to show that the experimental observation is generalisable to more than a specific tissue sample or cell line.  For this we need to show that the effect holds across multiple different samples.

The more different the samples are the stronger the case that can be made.  For example if an effect is shown to be consistent across a population of genetically identical mice this is not as strong as showing that the effect is the same in another different strain of mouse.  Even stronger would be using different rodents or even a completely different species altogether.

Experimenter replicates

Each experimenter introduces their own variation via differences in skill, patience and familiarity with a given assay.  Replication by multiple people shows that the result can be obtained by a different person using the same protocol, reagents and equipment as the original experiment.

For complicated or tricky experiments it is often common for a researcher to visit a lab which has the experiment working in order to learn first-hand the techniques used by the original experimenter to enable them to be able to reproduce an experiment on their own.

Method replicates

Finally, another approach to confirming your results is to use a different method entirely.  In most high impact papers it is often the case that an important observation may be shown in multiple different ways and in multiple model systems in order to demonstrate its robustness.

One simple example might be to show the change in regulation of a gene or pathway via detection using a whole genome screen (RNA-seq/microarray), quantitative RNA abundance (qRT-PCR), protein abundance (western blot) and via changes in localisation within the tissue (immunohistochemistry).  These methods may therefore be complimentary to one another and tell the same story but share little otherwise in common.  This may be extended to show the effect in a variety of tissues or model systems.

Laboratory replicates

Laboratory replicates are the gold standard of experimental replication and are used to demonstrate that the results of an experiment can be replicated by the scientific community at large.  When results are replicated by many different laboratories they come as close to the label of "truth" that science can reasonably apply.

Variation between labs and institutes can be induced by apparently minor differences in protocol, equipment, reagents, regulations, behaviour, strains of model system, batches of the same reagent and suppliers of equipment.

Summary

As you move up the replication hierarchy, the number of confounding variables will increase - your experiment will be less controlled.  But the results will be more generalisable and robust.  Ultimately the strength of your observation should exceed the noise introduced by any of the confounding variables we've discussed above in order to be accepted by the scientific community. Otherwise it just goes down in history as unreproducible.

But how easy should it be to reproduce results?  Methods sections may be incomplete and this not necessarily the authors fault; journals frequently impose word limits which may preclude full detail.  Reagents used may no longer be available and the replacement may not work in the same way.  And there is just as much chance that the original experiment is correct and the replication is wrong as there is of the reverse.  For a more in depth discussion see this post by Ian Dworkin.

It is good to see endeavours such as the reproducibility initiative set out to independently reproduce important papers.  In addition important papers will be reproduced simply because other labs will want to build on previous published results and will discover problems in reproducing it while they try to extend it.

This does, however, leave one problem.  Small papers, with less ground-breaking results, published in low-tier journals are less likely to be reproduced by other labs - they may not be as interesting for other labs to build on. As such their results may live on in science as a dogma that may persist for many years.  It is unclear to me how to address this final issue as there are currently very few incentives for scientists to reproduce results for their own sake.

The G Test and Bisulphite Sequencing DMRs

This is Part 4 in a series on Bisulphite Sequencing.
You can return to Part 3 (Bisulphite Sequencing Simple Visualisation).

Okay, so we have our bisulphite sequencing data on the UCSC genome browser. Lets assume we have two conditions CondA and CondB, and we have two replicates of each condition. We can see what appear to be changes from our visual inspection on the browser. Now what?

Well, we probably want to compute differentially methylated regions. With 1 replicate of each that's fairly straight forward for categorical data like the bisulphite seq data we have - we use fishers exact test. With replicates a simple approach is just to pool the two replicates together and do our fishers exact test on the pooled data, but this doesn't give us a very good idea of what's going on if the two replicates disagree for a given region.

Instead we use the G-test which can be calculated for any given contingency table with the following formula:

$$$$ G = 2 \sum_{i=0}^{r} \sum_{j=0}^{c} {O_{i,j} \ln(O_{i,j}/E_{i,j}) } $$$$
Where, $$$r$$$ and $$$c$$$ are the number of rows and columns in the contingency table, $$$O_{i,j}$$$ and $$$E_{i,j}$$$ are the Observed and Expected values for cell $$$i,j$$$ in the table. I've detailed how to implement the G-test for a 2x2 contingency table in Python previously.

The main selling point of the G-test, over a regular chi-square test, is that the G value is additive. Consider the following:

G-test 1	G-test 2
A B G-value C 100 70 = 7.1 D 35 50	A B G-value C 200 140 = 14.2 D 70 100

To find out where we have differential regions we first partition the genome into 2kb windows. There are large regions of the genome where there are no CpG's or, alternatively, where we have no sequencing coverage - we will skip those regions. We align our windows such that each window starts at an individual CpG and stops at the last CpG within 2kb of the start position.

Pooled G

We first compute a Pooled G which is the G-test performed on the pooled replicates. The contingency table would consist of columns representing each condition and rows representing methylated and unmethylated counts. The number of degrees of freedom is equal to $$$(R-1) \cdot (C-1)$$$ so as we are doing a single 2x2 contingency table this will always be equal to 1.

def pooledG(lmeth,lunmeth,rmeth,runmeth):   
    dof = 1
    pooledg = gtest(lmeth,lunmeth,rmeth,runmeth)
    return pooledg, dof, GtoP(pooledg,dof)

Total G

We then compute a G-value for each individual replicate and add them together. Each G-test we do adds 1 to the total number of degrees of freedom.

def totalG(data):
    dof = 0
    totalg = 0
    for lmeth,lunmeth,rmeth,runmeth in data:
            totalg += gtest(lmeth,lunmeth,rmeth,runmeth)
            dof+=1 
    return totalg, dof, GtoP(totalg,dof)

Heterogeneous G

If each of our three replicates reproduce exactly then Pooled G will be identical to Total G (due to the additive nature of G-test results). However, if the ratios are not identical then they will not match. The difference between the Total G-value and the Pooled G-value is the heterogeneous G-value and tells us if the difference between our replicates is significant (i.e. our replicates are not all doing the same thing.

def heterogenousG(totalg,totaldof,pooledg,pooleddof):
    heteroG = totalg-pooledg
    heterodof = totaldof-pooleddof
    return heteroG,heterodof,GtoP(heteroG,totaldof-pooleddof)

Putting it all together

Now, we can iterate through a file summarising the number of methylated and unmethylated reads at each CpG (described in a previous post) and compute the Pooled, Total and Heterogenous G-values (and corresponding p-values) for each genomic window.

import getopt
import sys
import csv
from itertools import izip_longest
from itertools import izip
from memoized import memoized

# sudo easy_install mpmath
import mpmath
#mpmath.mp.dps = 20 # decimal digits of precision

@memoized
def mpmathcdf(g,df,dps=10):
    mpmath.mp.dps = dps
    
    x,k = mpmath.mpf(g), mpmath.mpf(df)
    cdf = mpmath.gammainc(k/2, 0, x/2, regularized=True)
    
    # floating point precision insufficient, use more precision
    if cdf == 1.0:
        if dps > 4000:
            return cdf # give up after a certain point
        else:
            cdf = mpmathcdf(g,df,dps*2)
    return cdf

def GtoP(g,df):
    assert g >= 0, g
    return float(1-mpmathcdf(g,df))

import math

@memoized
def flnf(f):
    return f*math.log(f) if f>0.5 else 0

@memoized
def gtest(a,b,c,d):
    row1 = a+b
    row2 = c+d
    col1 = a+c
    col2 = b+d
    
    total = flnf(a+b+c+d)
    celltotals = flnf(a)+flnf(b)+flnf(c)+flnf(d)
    rowtotals = flnf(row1)+flnf(row2)
    coltotals = flnf(col1)+flnf(col2)
    
    # abs is necessary to account for float precision errors when doing the subtraction
    return abs(2*((celltotals + total)-(rowtotals+coltotals)))



# extract the pooled meth counts from the sample
def pooledMethCounts(data,covs,compare):
    lmethtotal = 0
    lunmethtotal = 0
    rmethtotal = 0
    runmethtotal = 0
    
    if len(compare)==2:
        # if we are given covariates to use
        covleft, covright = compare    
        for cov, (meth,unmeth) in izip(covs,grouper(2,data)): # extract in pairs of meth/unmeth
            if cov == covleft:
                lmethtotal += meth
                lunmethtotal += unmeth
            elif cov == covright:
                rmethtotal += meth
                runmethtotal += unmeth
    else:
        # if we have not been given them, assume that each adjacent sample (which is one pair) is one replicate
        for lmeth,lunmeth,rmeth,runmeth in grouper(4,data): # extract in quads (2 pairs) representing one replicate
            lmethtotal += lmeth
            lunmethtotal += lunmeth
            rmethtotal += rmeth
            runmethtotal += runmeth
        
    return lmethtotal,lunmethtotal,rmethtotal,runmethtotal


# extract individual replicate counts from the sample and return as a list of (lmeth,lunmeth,rmeth,runmeth)
# where l and r refer to the left and right cov in the compare array
# if compare array is empty assume that data is formatted as:
# lmeth1,lunmeth1,rmeth1,runmeth1,lmeth2,lunmeth2,rmeth2,runmeth2 etc
def covReplicateMethCounts(data,covs,compare):
    if len(compare)==2:
        covleft, covright = compare
        
        lreplicates = []
        rreplicates = []
    
        for cov, (meth,unmeth) in izip(covs,grouper(2,data)): # extract in pairs of meth/unmeth
            if cov == covleft:
                lreplicates.append((meth,unmeth))
            elif cov == covright:
                rreplicates.append((meth,unmeth))

        #return [(lmeth,lunmeth,rmeth,runmeth),(),(),...]    
        return [(a,b,c,d) for (a,b),(c,d) in izip(lreplicates,rreplicates)]
    else:
        # assume that each pair of samples (i.e. 4 columns) in the input is one replicate
        # in this case our input file is in the right order and we just need to split it up.
        return grouper(4,data)


# total G: at least some of the data is different
# 1 degree of freedom per replicate (i.e. 3 in total), add G's from each seperate test
def totalG(data,covs,compare):
    dof = 0
    totalg = 0
    for lmeth,lunmeth,rmeth,runmeth in covReplicateMethCounts(data,covs,compare): # extract in quads (2 pairs)
            totalg += gtest(lmeth,lunmeth,rmeth,runmeth)
            dof+=1 
    assert totalg >= 0
    return totalg, dof, GtoP(totalg,dof)

# pooled G: the data as a whole is different
# 1 degree of freedom, pool results from all replicates and do 1 2x2 table
def pooledG(data,covs,compare):    
    lmeth,lunmeth,rmeth,runmeth = pooledMethCounts(data,covs,compare)
    
    dof = 1
    
    pooledg = gtest(lmeth,lunmeth,rmeth,runmeth)
    
    assert pooledg >= 0
    
    return pooledg, dof, GtoP(pooledg,dof)

# there is evidence that they are significantly different from each other
# heterogeneity G: total G - pooled G, df = 3-1 = 2
def heterogeneityG(totalg,totaldof,pooledg,pooleddof):
    heteroG = max(totalg-pooledg,0)
    heterodof = totaldof-pooleddof
    return heteroG,heterodof,GtoP(heteroG,totaldof-pooleddof)


def grouper(n, iterable, fillvalue=None):
    "grouper(3, 'ABCDEFG', 'x') --> ABC DEF Gxx"
    args = [iter(iterable)] * n
    return izip_longest(fillvalue=fillvalue, *args)

def unpackLine(chrm,coord,*data):
    return chrm.strip(), int(coord), [int(d) for d in data]

def extractLine(line):
    chrm,coord,data = unpackLine(*line)
    if not chrm.startswith("chr"):
        chrm = "chr"+chrm
    return (chrm,coord,data)


    
if __name__ == '__main__':
    try:
        opts, args = getopt.getopt(sys.argv[1:], "", ["combined=","cov=","compare="])
    except getopt.GetoptError, err:
        # print help information and exit:
        print str(err) # will print something like "option -a not recognized"
        sys.exit(2)
    
    infile = None
    covs = None
    compare = None
    
    for o, a in opts:
        if o=="--combined":
            infile = a
            print "combined", a
        elif o=="--cov":
            covs = a.split(",")
            print covs
        elif o=="--compare":
            compare = a.split(",")
            print compare
            assert len(compare)==2
    
    assert infile != None
    
    # we either have compare and covs or neither
    assert compare == None or len(compare)==2
    if compare == None: assert covs == None
    if len(compare)==2: assert covs != None
    
    methfile = csv.reader(open(infile, "r"), delimiter="\t")
    
    # ---    
    # windows
    
    if compare != None:
        leftcov,rightcov = compare
        windows = csv.writer(open(infile+"."+leftcov+"-vs-"+rightcov+".windows.bedGraph","w"),delimiter='\t')
        percent = csv.writer(open(infile+"."+leftcov+"-vs-"+rightcov+".percent.windows.bedGraph","w"),delimiter='\t')
    else:
        windows = csv.writer(open(infile+".windows.bedGraph","w"),delimiter='\t')
        percent = csv.writer(open(infile+".percent.windows.bedGraph","w"),delimiter='\t')
    
    windowSize = 2000
    
    currentWindowPos = None
    currentChr = None
    
    cs = 0
    dataCount = None
    
    def writeWindow(chrm,pos,epos):
        global dataCount
        global cs
        global windows
        global percent
        
        lmethCount,lunmethCount,rmethCount,runmethCount = pooledMethCounts(dataCount,covs,compare)
        
        if (lmethCount + lunmethCount) == 0 or (rmethCount + runmethCount) == 0:
            print "Unprintable window:",chrm, pos, epos, lmethCount, lunmethCount, rmethCount, runmethCount
            return
        
        lPercentage = (float(lmethCount)/float(lmethCount+lunmethCount)) * 100.0
        rPercentage = (float(rmethCount)/float(rmethCount+runmethCount)) * 100.0
        
        total,totaldof,totalp = totalG(dataCount,covs,compare)
        pooled,pooleddof,pooledp = pooledG(dataCount,covs,compare)
        hetero,heterodof,heterop = heterogeneityG(total,totaldof,pooled,pooleddof)
        
        windows.writerow([chrm,pos,epos+1,'1' if rPercentage > lPercentage else '-1',totalp,pooledp,heterop,cs])
        
        percent.writerow([chrm,pos,epos+1,lPercentage,rPercentage])         
        
        dataCount = None
        cs = 0

    lastCoordCounted = None
    # the actual work here
    for line in methfile:
        
        chrm,coord,data = extractLine(line)

        if currentChr == None:
            currentChr = chrm
            currentWindowPos = coord
            lastCoordCounted = coord
        else:
            # always write a window if we change chrm
            if chrm != currentChr:
                writeWindow(currentChr,currentWindowPos,lastCoordCounted)
                currentChr = chrm
                currentWindowPos = coord
                
            # write a window if the next cpg is outside the current window
            elif coord - currentWindowPos > windowSize:
                writeWindow(currentChr,currentWindowPos,lastCoordCounted)
                currentChr = chrm
                currentWindowPos = coord
                
            # otherwise dont write any window (the current cpg is in the window)
        
        ####
        # add data to existing data count
        ####
        if dataCount == None:
            dataCount = data
        else:
            for index,d in enumerate(data):
                dataCount[index] += d
        lastCoordCounted = coord
        
        # inc number of c's counted
        cs += 1
        
    # after we write a window there is always at least one unmeasured coord after it so we have one more window to write
    writeWindow(currentChr,currentWindowPos,lastCoordCounted)

Note that the above script relies upon the Memoized decorator.

Executed as:

python replicatesGTest.py \
--combined "Conditions.1.and.2.CpG_context.aggregate" \
--cov Condition1,Condition2,Condition1,Condition2,Condition1,Condition2
--compare Condition1,Condition2 

Where --cov lists the order of the conditions in the file and --cov indicates which conditions should be compared.

For each window, this script outputs a tab separated file containing the chromosome,start and stop position of the window,'1' if it is "increasing" otherwise '-1' and p-values for computed from the Total, Pooled ahd Hetero G computations as well as the number of methylation sites considered in the window.

Note that the p-values generated are uncorrected for multiple testing and should be FDR corrected. I've previously described a suitable approach for large files such as these.

Differentially methylated regions can then be defined as regions of adjacent windows with a FDR adjusted p-value less than or equal to a fixed level (i.e. 0.05 FDR) that change in the same direction.

The G-Test and Python

The G-Test is a statistical test which can be used much like a chi-squared test. It is defined as: $$$$ G = 2 \sum_{i=0}^{r} \sum_{j=0}^{c} {O_{i,j} \ln(O_{i,j}/E_{i,j}) } $$$$ Where, $$$r$$$ and $$$c$$$ are the number of rows and columns in the contingency table and $$$O_{i,j}$$$ and $$$E_{i,j}$$$ are the Observed and Expected values for cell $$$i,j$$$ in the table.

To make a straightforward implementation for it in Python we first do a bit of math. For a 2x2 contingency table:

$$$ G = 2 \Bigg({O_{1,1} \ln(\frac{O_{1,1}}{E_{1,1}})} + {O_{1,2} \ln(\frac{O_{1,2}}{E_{1,2}})} + {O_{2,1} \ln(\frac{O_{2,1}}{E_{2,1}})} + {O_{2,2} \ln(\frac{O_{2,2}}{E_{2,2}})} \Bigg) $$$

Expand via log equivalences:

$$$ G = 2 \Bigg( $$$	$$$ \bigg( {O_{1,1} \ln(O_{1,1}) - O_{1,1} \ln(E_{1,1})} \bigg) + \bigg( {O_{1,2} \ln(O_{1,2}) - O_{1,2} \ln(E_{1,2})} \bigg) $$$
	$$$ + \bigg( {O_{2,1} \ln(O_{2,1}) - O_{2,1} \ln(E_{2,1})} \bigg) + \bigg( {O_{2,2} \ln(O_{2,2}) - O_{2,2} \ln(E_{2,2})} \bigg) \Bigg) $$$

Group Observed vs Expected together:

$$$ G = 2 \Bigg( $$$	$$$ \bigg( O_{1,1} \ln(O_{1,1}) + O_{1,2} \ln(O_{1,2}) + O_{2,1} \ln(O_{2,1}) + O_{2,2} \ln(O_{1,2}) \bigg)$$$
	$$$ - \bigg( O_{1,1} \ln(E_{1,1}) + O_{1,2} \ln(E_{1,2}) + O_{2,1} \ln(E_{2,1}) + O_{2,2} \ln(E_{2,2}) \Bigg) $$$

For a 2x2 contingency table; $$$E_{i,j} = \frac{T_{i} \cdot T_{j}}{T} $$$, where $$$T_{i}$$$ and $$$T_{j}$$$ are the totals for the row and column of cell $$$E_{i,j}$$$ and $$$T$$$ is the total for all cells in the table. Specifically, $$$$ \ln(E_{1,1}) = \ln \Bigg( \frac{ (O_{1,1}+O_{1,2}) \cdot (O_{1,1}+O_{2,1}) }{ O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} } \Bigg) $$$$ $$$$ \ln(E_{1,2}) = \ln \Bigg( \frac{ (O_{1,1}+O_{1,2}) \cdot (O_{1,2}+O_{2,2}) }{ O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} } \Bigg) $$$$ $$$$ \ln(E_{2,1}) = \ln \Bigg( \frac{ (O_{2,1}+O_{2,2}) \cdot (O_{1,1}+O_{2,1}) }{ O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} } \Bigg) $$$$ $$$$ \ln(E_{2,2}) = \ln \Bigg( \frac{ (O_{2,1}+O_{2,2}) \cdot (O_{1,2}+O_{2,2}) }{ O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} } \Bigg) $$$$
We then substitute these into our equation for G.

$$$ G = 2 \Bigg( $$$	$$$\bigg( O_{1,1} \ln(O_{1,1}) + O_{1,2} \ln(O_{1,2}) + O_{2,1} \ln(O_{2,1}) + O_{2,2} \ln(O_{1,2}) \bigg) - $$$
	$$$ \bigg( O_{1,1} \ln \Big( \frac{ (O_{1,1}+O_{1,2}) \cdot (O_{1,1}+O_{2,1}) }{ O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} } \Big) + O_{1,2} \ln \Big( \frac{ (O_{1,1}+O_{1,2}) \cdot (O_{1,2}+O_{2,2}) }{ O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} } \Big) + $$$
	$$$ O_{2,1} \ln \Big( \frac{ (O_{2,1}+O_{2,2}) \cdot (O_{1,1}+O_{2,1}) }{ O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} } \Big) + O_{2,2} \ln \Big( \frac{ (O_{2,1}+O_{2,2}) \cdot (O_{1,2}+O_{2,2}) }{ O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} } \Big) \bigg) \Bigg) $$$

Another log equivalence gives us this:

$$$ G = 2 \Bigg( $$$	$$$\bigg( O_{1,1} \ln(O_{1,1}) + O_{1,2} \ln(O_{1,2}) + O_{2,1} \ln(O_{2,1}) + O_{2,2} \ln(O_{1,2}) \bigg) - $$$
	$$$ \bigg( O_{1,1} \ln ( (O_{1,1}+O_{1,2}) \cdot (O_{1,1}+O_{2,1}) ) - O_{1,1} \ln ( O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} ) + $$$
	$$$ O_{1,2} \ln ( (O_{1,1}+O_{1,2}) \cdot (O_{1,2}+O_{2,2}) ) - O_{1,2} \ln ( O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} ) + $$$
	$$$ O_{2,1} \ln ( (O_{2,1}+O_{2,2}) \cdot (O_{1,1}+O_{2,1}) ) - O_{2,1} \ln ( O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} ) + $$$
	$$$ O_{2,2} \ln ( (O_{2,1}+O_{2,2}) \cdot (O_{1,2}+O_{2,2}) ) - O_{2,2} \ln ( O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} ) \bigg) \Bigg) $$$

Group common factor of $$$\ln ( O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2} )$$$:

$$$ G = 2 \Bigg( $$$	$$$ \bigg( O_{1,1} \ln(O_{1,1}) + O_{1,2} \ln(O_{1,2}) + O_{2,1} \ln(O_{2,1}) + O_{2,2} \ln(O_{1,2}) \bigg) +$$$
	$$$ \bigg( (O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2}) \cdot \ln(O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2}) \bigg) - $$$
	$$$ \bigg( O_{1,1} \ln \big( (O_{1,1}+O_{1,2}) \cdot (O_{1,1}+O_{2,1}) \big) + O_{1,2} \ln \big( (O_{1,1}+O_{1,2}) \cdot (O_{1,2}+O_{2,2}) \big) + $$$
	$$$ O_{2,1} \ln \big( (O_{2,1}+O_{2,2}) \cdot (O_{1,1}+O_{2,1}) \big) + O_{2,2} \ln \big( (O_{2,1}+O_{2,2}) \cdot (O_{1,2}+O_{2,2}) \big) \bigg) \Bigg) $$$

More log equivalences:

$$$ G = 2 \Bigg( $$$	$$$ \bigg( O_{1,1} \ln(O_{1,1}) + O_{1,2} \ln(O_{1,2}) + O_{2,1} \ln(O_{2,1}) + O_{2,2} \ln(O_{1,2}) \bigg) + $$$
	$$$ \bigg( (O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2}) \cdot \ln(O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2}) \bigg) -$$$
	$$$ \bigg( O_{1,1} \ln (O_{1,1}+O_{1,2}) + O_{1,1} \ln (O_{1,1}+O_{2,1}) + O_{1,2} \ln (O_{1,1}+O_{1,2}) + O_{1,2} \ln (O_{1,2}+O_{2,2}) + $$$
	$$$ O_{2,1} \ln (O_{2,1}+O_{2,2}) + O_{2,1} \ln (O_{1,1}+O_{2,1}) + O_{2,2} \ln (O_{2,1}+O_{2,2}) + O_{2,2} \ln (O_{1,2}+O_{2,2}) \bigg) \Bigg) $$$

Group common factors of $$$\ln (O_{1,1}+O_{1,2})$$$, $$$\ln (O_{1,1}+O_{2,1})$$$ etc. Yielding:

$$$ G = 2 \Bigg( $$$	$$$ \bigg( O_{1,1} \ln(O_{1,1}) + O_{1,2} \ln(O_{1,2}) + O_{2,1} \ln(O_{2,1}) + O_{2,2} \ln(O_{1,2}) \bigg) $$$
	$$$ + \bigg( (O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2}) \cdot \ln(O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2}) \bigg) $$$
	$$$ - \bigg( (O_{1,1} + O_{1,2}) \ln (O_{1,1}+O_{1,2}) + (O_{2,1} + O_{2,2}) \ln (O_{2,1}+O_{2,2}) \bigg) $$$
	$$$ - \bigg( (O_{1,1} + O_{2,1}) \ln (O_{1,1}+O_{2,1}) + (O_{1,2} + O_{2,2}) \ln (O_{1,2}+O_{2,2}) \bigg) \Bigg) $$$

We can then summarise the four parts of the above equation as follows:
$$$$ celltotals = O_{1,1} \ln(O_{1,1}) + O_{1,2} \ln(O_{1,2}) + O_{2,1} \ln(O_{2,1}) + O_{2,2} \ln(O_{1,2}) $$$$ $$$$ total = (O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2}) \ln(O_{1,1} + O_{1,2} + O_{2,1} + O_{2,2}) $$$$ $$$$ rowtotals = (O_{1,1} + O_{1,2}) \ln (O_{1,1}+O_{1,2}) + (O_{2,1} + O_{2,2}) \ln (O_{2,1}+O_{2,2}) $$$$ $$$$ columntotals = (O_{1,1} + O_{2,1}) \ln (O_{1,1}+O_{2,1}) + (O_{1,2} + O_{2,2}) \ln (O_{1,2}+O_{2,2}) $$$$ where: $$$$ G = 2 \big(celltotals + total - (rowtotals + columntotals) \big) $$$$ If we assign $$$a = O_{1,1}, b = O_{1,2}, c = O_{2,1}, d = O_{2,2}$$$ then we can then implement as follows in Python:

import math

def flnf(f):
    return f*math.log(f) if f>0.5 else 0

def gtest(a,b,c,d):
    row1 = a+b
    row2 = c+d
    col1 = a+c
    col2 = b+d
    
    total = flnf(a+b+c+d)
    celltotals = flnf(a)+flnf(b)+flnf(c)+flnf(d)
    rowtotals = flnf(row1)+flnf(row2)
    coltotals = flnf(col1)+flnf(col2)
    
    return 2*(celltotals + total-(rowtotals+coltotals))

We then probably want to convert our G-value into a P-value. The G-test approximates a chi squared distribution and has the same number of degrees of freedom.

If the calculated chi-squared distribution cumulative distribution function is equal to exactly 1 (i.e. a p-value of exactly 0) then we increase the precision and try again. This means that we can find the correct order of magnitude for our p-value (which is good for when we FDR correct these p-values later on) while minimising the number of calculations we need to do (the majority of conversions don't need 4000 decimal places computed). ($$$g$$$ is the G-value and $$$df$$$ is the degrees of freedom - 1 for a 2x2 table).

import mpmath

def mpmathcdf(g,df,dps=10):
    mpmath.mp.dps = dps
    
    x,k = mpmath.mpf(g), mpmath.mpf(df)
    cdf = mpmath.gammainc(k/2, 0, x/2, regularized=True)
    
    # floating point precision insufficient, use more precision
    if cdf == 1.0:
        if dps > 4000:
            return cdf # give up after a certain point
        else:
            cdf = mpmathcdf(g,df,dps*2)
    return cdf

def GtoP(g,df):
    assert g >= 0, g
    return float(1-mpmathcdf(g,df))

Update:

Following on from the comments below I've written up a generalised version of the G-test for any sized contingency table which uses the trick from above. I've not proven explicitly that this is necessarily generalisable for any sized table but I'm pretty sure it is.

def gtest(a):
    rowtotals = []
    coltotals = [0]*len(a[0])
    cells = []
    for row in a:
        rowtotals.append(sum(row))
        for index,col in enumerate(row):
            coltotals[index] += col
            cells.append(col)
    return 2*(math.fsum([flnf(x) for x in cells]) + flnf(sum(cells)) - ( math.fsum([flnf(x) for x in rowtotals]) + math.fsum([flnf(x) for x in coltotals]) ))

For a table with 2 columns and 3 rows this can then be called as follows:

gtest([[268,807],
       [199,759],
       [42,184]])

> 7.300817075862142

Again, because I've not proven this will always work it should, of course, be used at your own risk. That said, the same technique is used for up to 10 columns and 50 rows in the G-test spreadsheet at the Handbook for Biological Statistics so it's probably safe at least that far.

Bisulphite Sequencing Simple Visualisation (Multiple Samples)

This is Part 3 in a series on Bisulphite Sequencing.
You can return to Part 2 (Using the Binomial Distribution in Bisulphite Sequencing). or skip to Part 4 (The G Test and Bisulphite Sequencing DMRs).

Jumping back to bisulphite sequencing analysis for a bit.  After we have summarised our data by individual CpG we probably want to do something useful with it.

First up, lets just display it on the UCSC genome browser.  When we display bisulphite sequening data on UCSC we probably want something like this below:

 

We also want to filter out low confidence CpGs (those with less than a certain number of reads). bismarkToBedGraph does something pretty much like this.

However, it is important that when we filter a particular CpG from any given sample we should also filter it from the other samples displayed at the same time - otherwise we give a misleading indication that there is 0% methylation in the filtered sample and a non-negative amount of methylation in the unfiltered sample.

To address this I made a short script that can take multiple replicates/samples of bisulphite sequencing data, summarised by individual CpGs, and output bedGraph files such that the same CpGs are always reported based on coverage.

import getopt
import sys
import csv
from itertools import izip_longest

class CommentException(Exception):
    pass

def grouper(n, iterable, fillvalue=None):
    "grouper(3, 'ABCDEFG', 'x') --> ABC DEF Gxx"
    args = [iter(iterable)] * n
    return izip_longest(fillvalue=fillvalue, *args)

def unpackLine(chrm,coord,*data):
    return chrm.strip(), int(coord), [int(d) for d in data]

def extractLine(line):
    if line[0].startswith("#"):
        raise CommentException()
    chrm,coord,data = unpackLine(*line)

    if not chrm.startswith("chr"):
        chrm = "chr"+chrm
    return (chrm,coord,data)
    
if __name__ == '__main__':
    try:
        opts, args = getopt.getopt(sys.argv[1:], "", ["combined=","suffixes="])
    except getopt.GetoptError, err:
        # print help information and exit:
        print str(err) # will print something like "option -a not recognized"
        sys.exit(2)
    
    infile = None
    suffixes = None
    rightsuffix = None
    
    for o, a in opts:
        if o=="--combined":
            infile = a
            print "combined", a
        elif o=="--suffixes":
            suffixes = a.split(",")
            print "Suffix", suffixes

    
    assert infile != None
    assert suffixes != None
    
    methfile = csv.reader(open(infile, "r"), delimiter="\t")
    
    files = {}
    
    for suffix in suffixes:
        percentage = csv.writer(open(infile+"-"+suffix+".percent.bedGraph","w"),delimiter='\t')
        coverage = csv.writer(open(infile+"-"+suffix+".coverage.bedGraph","w"),delimiter='\t')
        files[suffix]=(percentage,coverage)
    
    # ---
    # for each
    # coverage
    # percentage
    
    minReadsForPercentage = 5
    minSamplesWithCoverage = 1

    for line in methfile:
        try:
            (chrm,coord,data) = extractLine(line)
        except CommentException:
            continue
        
        percentages = []
        coverages = []
        
        for meth,unmeth in grouper(2,data):
            coverage = meth + unmeth
            if coverage == 0:
                percentage = 0
            else:           
                percentage = (float(meth)/float(meth+unmeth)) * 100.0
            percentages.append(percentage)
            coverages.append(coverage)
    
        satisfycoveragecriteria = 0
        for coverage in coverages:
            if coverage >= minReadsForPercentage:
                satisfycoveragecriteria += 1
        if satisfycoveragecriteria < minSamplesWithCoverage:
            continue

        for index,(percentage,coverage) in enumerate(izip_longest(percentages,coverages)):
            
            percentfile,coveragefile = files[suffixes[index]]
            percentfile.writerow([chrm,coord,coord+1,percentage])
            coveragefile.writerow([chrm,coord,coord+1,coverage])
            

Executed as:

python bisulphiteToBedGraph.py \
--combined "Samples.1.and.2.CpG_context.aggregate" \
--suffixes Sample1,Sample2,Sample3,Sample4 

You can then use bedGraphToBigWig to create bigWig files suitable for UCSC custom track / track hubs.

qPCR normalisation

This post will discuss the normalisation of qPCR results using both the Delta Delta CT (Livak) and Standard Curve (Pfaffl) methods as applied to qPCR of RNA and ChIP.  It will also discuss some of the common pitfalls when considering replicates of qPCR data.

While this isn't a cutting edge technique, the motivation for this post is the number of qPCR spreadsheets I see that do this wrongly.

Delta Delta CT

The Livak method is more commonly known as the "Delta Delta CT" (ΔΔCT). The Delta Delta CT method makes one important assumption about the PCR, namely, the amplification efficiencies of the reference control gene and the target gene of interest must be approximately equal.  Specifically Delta Delta CT assumes that each PCR cycle will exactly double the amount of material in your sample (amplification efficiency = 100%).

$$$ ΔΔCT = ΔCT (treated sample) - ΔCT (untreated sample) $$$

where $$$ ΔCT(sample) = CT(target) - CT(ref) $$$, therefore

$$$ ΔΔCT = (CT(target,untreated) - CT(ref,untreated)) - (CT(target,treated) - CT(ref,treated)) $$$

where

$$$CT(target,untreated)$$$ = CT value of gene of interest in untreated sample
$$$CT(ref,untreated)$$$ = CT value of control gene in untreated sample
$$$CT(target,treated)$$$ = CT value of gene of interest in treated sample
$$$CT(ref,treated)$$$ =  CT value of control gene in treated sample

We can then calculate the ratio of our target gene in our treated sample relative to our untreated sample by taking $$$2^{ΔΔCT}$$$.

A quick worked example:

	Untreated	Treated
Ref Gene	16.17	15.895
Target Gene	21.225	19.763

$$$$ΔΔCT = (CT(target,untreated) - CT(ref,untreated)) - (CT(target,treated) - CT(ref,treated))$$$$
$$$$ΔΔCT = (21.225 - 16.17) - (19.763 - 15.895)$$$$
$$$$ΔΔCT = (5.055) - (3.868)$$$$
$$$$ΔΔCT = 1.187$$$$
$$$$2^{ΔΔCT} = 2^{1.187} = 2.277$$$$

So our gene of interest is increased by 2.277 times in our treated sample versus our untreated sample.

The exact order that you do the subtraction in actually doesn't make a huge difference and you'll probably see other people do it slightly differently.  Consider these possibilities:

ΔUntreated vs ΔTreated

$$$ΔΔCT = (CT(target,untreated) - CT(ref,untreated)) - (CT(target,treated) - CT(ref,treated))$$$
$$$ΔΔCT = (21.225 - 16.17) - (19.763 - 15.895)$$$
$$$ΔΔCT = 1.187$$$

$$$ΔΔCT = (CT(ref,treated) - CT(target,treated)) - (CT(ref,untreated) - CT(target,untreated))$$$
$$$ΔΔCT = (15.895 - 19.763) - (16.17 - 21.225)$$$
$$$ΔΔCT = 1.187$$$

$$$ΔΔCT = (CT(ref,untreated) - CT(target,untreated)) - (CT(ref,treated) - CT(target,treated))$$$
$$$ΔΔCT = (16.17 - 21.225) - (15.895 - 19.763)$$$
$$$ΔΔCT = -1.187$$$

$$$ΔΔCT = (CT(target,treated) - CT(ref,treated)) - (CT(target,untreated) - CT(ref,untreated))$$$
$$$ΔΔCT = (19.763 - 15.895) - (21.225 - 16.17)$$$
$$$ΔΔCT = -1.187$$$


ΔReference Gene vs ΔTarget Gene


$$$ΔΔCT = (CT(target,untreated) - CT(target,treated)) - (CT(ref,untreated) - CT(ref,treated))$$$
$$$ΔΔCT = (21.225 - 19.763) - (16.17 - 15.895)$$$
$$$ΔΔCT = 1.187$$$

$$$ΔΔCT = (CT(ref,treated) - CT(ref,untreated)) - (CT(target,treated) - CT(target,untreated))$$$
$$$ΔΔCT = (15.895 - 16.17) - (19.763 - 21.225)$$$
$$$ΔΔCT = 1.187$$$

$$$ΔΔCT = (CT(ref,untreated) - CT(ref,treated)) - (CT(target,untreated) - CT(target,treated))$$$
$$$ΔΔCT = (16.17 - 15.895) - (21.225 - 19.763)$$$
$$$ΔΔCT = -1.187$$$

$$$ΔΔCT = (CT(target,treated) - CT(target,untreated)) - (CT(ref,treated) - CT(ref,untreated))$$$
$$$ΔΔCT = (19.763 - 21.225) - (15.895 - 16.17)$$$
$$$ΔΔCT = -1.187$$$

As long as you stay consistent with the two ΔCT subtractions (i.e. always subtract treated from untreated, or reference gene from control gene, or vice versa) then the magnitude of the ΔΔCT part will always be the same.  The only thing that will change is the sign.

This is why you'll see some people will calculate the expression ratio as $$$2^{ΔΔCT}$$$ and others will do it as $$$2^{-ΔΔCT}$$$.  The difference is basically just how they set up their initial equation - effectively which direction they are comparing the samples.

To see why Delta Delta CT actually works we have to consider what's actually going on under the hood.

The absolute amount of material that we obtain through PCR for each sample for each primer pair is inversely proportional to $$$2^{CT}$$$.  We normalise our genes to a reference gene within each sample to ensure that we don't have any systematic errors due to differences between each sample (an internal control).

So the ratio of target gene to reference gene in each sample is therefore $$$2^{CT(target)} / 2^{CT(ref)}$$$.

However, because $$$\frac{b^c}{b^d} = b^{c-d}$$$ we can rewrite this as $$$2^{CT(target) - CT(ref)}$$$.

We then calculate the ratio between our two sample by calculating the quotient between the ratio of target gene to reference gene between the two samples as such:

$$$$Ratio = {2^{CT(target,untreated) - CT(ref,untreated)} \over 2^{CT(target,treated) - CT(ref,treated)}}$$$$

which by the same identity rule we applied before equals our ΔΔCT equation:

$$$(CT(target,untreated) - CT(ref,untreated)) - (CT(target,treated) - CT(ref,treated))$$$.

Standard Curve

An improvement to the Delta Delta CT method was introduced by Pfaffl to account for PCR efficiency curves deviating from the theoretical 100% efficient reaction.

To measure how efficient our PCR is for a given amplicon we run a template dilution series and see how closely our idealised PCR compares to real life.

If we run a dilution series of (0.25, 0.5, 1, 2) we would expect that there would be a one CT difference between each sample in the ideal 100% efficient reaction as shown:

CT Value	Concentration
36	0.25
35	0.5
34	1
33	2

However, if our actual measured CT values indicate a larger difference then our PCR reaction has been less efficient than we hoped.

CT Value	Concentration
36	0.25
34.9	0.5
33.8	1
32.7	2

We can work out exactly how much less efficient by comparing the CT values and the log of the Concentration.

We can do this on any log scale you like although commonly it'll be done on either $$$log_2$$$ or $$$log_{10}$$$ scales.  The result will come out the same either way.  We will use $$$log_2$$$ from now on since it fits well with the property of PCR doublings.

What we are interested in is the slope of the trend line.  In the case above the slope is -1.1.  We can then work out the efficiency of the reaction as

$$$Efficency = 2^{-1/slope} = 2^{-1/-1.1} = 1.878$$$

Therefore, for each PCR reaction we generate 1.878 copies of our template rather than, the theoretical, 2 copies in the ideal case.  The Efficiency is often then represented as a scale between 0-1 which is obtainable by subtracting 1 from the calculated efficiency above.

If we do a standard curve for each primer set we have (reference gene and target gene) then we can incorporate them into our Delta Delta CT equation to get:

$$$$Ratio = {Efficency(Target)^{CT(target,untreated) - CT(target,treated)} \over Efficency(Ref)^{CT(ref,untreated) - CT(ref,treated)}}$$$$

Note that the order of subtraction matters more here as we make sure that the the exponent of each calculated efficiency contains only the CT's which were produced by that primer pair.

ChIP-PCR

Unlike in RT-PCR for gene expression quantitation, ChIP-PCR will use a single primer pair per region of interest.  However, we will then usually also include an Input sample which the ChIP sample is compared with.

Input usually comprises a huge amount of DNA so it is usually necessary to take a subset of the Input as our actual sample to PCR.  The amount that is actually used may be between 1% and 10%.

To account for this we should apply an input adjustment.  This involves calculating a dilution factor which is equal to $$$1/ {Fraction Input}$$$.  For example if you have 1% input then your dilution factor (DF) is 1/0.01 = 100.  We then calculate our CT correction factor by calculating $$$log_{Efficiency}(Dilution Factor)$$$.

Worked example:  5% input is a DF of 1/0.05 = 20.  For the standard curve described above this is a CT correction of $$$log_{1.878}(20) = 4.75$$$.  This is then subtracted from each of the Input CTs before continuing as per the Standard Curve approach described above.

Because we only have a single primer pair we can use the same efficiency for the PCR throughout which allows us to simplify the Standard Curve approach to $$$Efficiency^{ΔΔCT}$$$.

Often you'll want to represent your result as a percent of input and this can be calculated for each condition as $$$Efficiency^{ΔCT}$$$.

Replicates & Error Propagation

One place that a number of mistakes seem to creep in is the treatment of replicates within PCR experiments.

The most frequent mistake I've seen is the use of the wrong type of mean when calculating the average ratio.  The key fact to remember is to always use the arithmetic mean on anything on a linear scale and always to use the geometric mean on anything on an exponential scale.

More concisely, if it's CT values (or differences thereof), then use an arithmetic mean.  If it's concentration values (anything that is $$$Efficiency^{CT}$$$) then use the geometric mean.

I also frequently encounter incorrect treatment of error bars.  Often people will take the standard deviation (or standard error) of concentration data, or ratios, and depict them directly in their bar charts.  However, these metrics assume normally distributed data which is only the case for the CT values themselves, not the ratios or concentrations.  Briefly, if your y axis on your chart is linear scale and your error bars are the same on both sides then this is wrong.

Finally we should deal with error propagation.  The error in your experiment is composed of the errors of $$$(Untreated,Ref) + (Untreated,Target) + (Treated,Ref) + (Treated,Target)$$$.  This error will usually be more than the error implied by taking the standard error of the ΔΔCT values for each replicate.  However, for uncorrelated variables we can propagate additive errors using the formula:

$$$Error(a+b) = \sqrt{ Error(a)^2 + Error(b)^2 }$$$

This works well for delta delta CT as the error is just the product of multiple additive errors.  However, for standard curve approaches we also have error from the Efficiency values we calculated for our curve and this can't be expressed as an additive factor.

Instead we need to use a Taylor series to propogate the error.  This allows for all six sources of variance (4x CTs + 2x Efficiencies) to be included in the final error calculation.

Control Gene Choice

One final factor is the choice of a suitable housekeeping gene as a control.  If you choose a reference housekeeping gene that changes wildly in between your untreated and treated samples then the results of your target gene compared to this gene will be wrong.

One approach to reduce the effect of this is to use the geometric mean of multiple housekeeping genes as your reference instead of choosing one.  Even still, it's important to carefully choose your reference genes for stability in your particular experiment.

Software

Another approach is just to use some of the software that's out there already.  One that's well used is REST 2009 which supports virtually anything you'll want to do.  Similarly there are open source solutions such as pyQPCR.  If you are willing to pay money you can also use something like GenEx.

If you do decide to make your own spreadsheet you should, at the very least, confirm that the answers you get from there are the same as the answers that you get from these programs.

I've uploaded a spreadsheet which illustrates most of the things I've talked about in this post.  It has examples for calculating standard curves, ΔΔCT, Standard Curve and Input Correction for ChIP-PCR.  It also has worked examples for error propagation for both ΔΔCT (via simple additive error propagation) and for Standard Curves (via a taylor series).

Realistically though, for almost all cases, and particularly anything rtPCR related, I recommend using something off the shelf like REST 2009.  There aren't many reasons you need to make your own spreadsheets - unless of course you are trying to explain how PCR normalisation works in a blog post.

Note that I've previously had errors in this spreadsheet myself.  I take this as a sign of just how easy it is to make these mistakes and also a reminder that there could well be errors still lurking in this sheet (and in any other spreadsheet or software you've used). Thanks most recently to Duncan Brian (UCL) for highlighting that the SE from the Taylor Series I took from REST384 was inversely correlated to the SE of the individual components. I've updated the sheet to include both the taylor series which matches the output of REST 384 and also the Taylor series described in the Gene Quantification Platform.

References

Gene Quantification Platform, Real Time PCR amended, A useful new approach? Statistical problems? http://www.gene-quantification.com/avery-rel-pcr-errors.pdf, Last Accessed 2017.

Livak, Kenneth J., and Thomas D. Schmittgen. Analysis of Relative Gene Expression Data Using Real-Time Quantitative PCR and the $$$2^{-ΔΔCT}$$$ Method. Methods 25.4 (2001).

Pfaffl, Michael W. A new mathematical model for relative quantification in real-time RT–PCR. Nucleic Acids Research 29.9 (2001).

Vandesompele, Jo, et al. Accurate normalization of real-time quantitative RT-PCR data by geometric averaging of multiple internal control genes. Genome biology 3.7 (2002).